Nhắc đến Pierre de Fermat là nhắc đến một nhà toán học vĩ đại người Pháp. Ông là cha đẻ của lý thuyết số hiện đại, trong đó có hai định lý nổi tiếng: định lý nhỏ Fermat và định lý lớn Fermat hay còn gọi là định lý cuối cùng của Fermat.
Pierre de Fermat sinh ngày 17/8/1601 tại Beaumont-de-Lomagne, Pháp trong một gia đình khá giả. Ông học ở Toulouse về luật dân sự, sau đó làm chánh án. Tuy vậy, Fermat lại vô cùng say mê toán học với thói quen nổi tiếng là ghi các ghi chú bên lề các quyển sách.

Nhà toán học Pierre de Fermat.
Nhà nghiên cứu lịch sử toán học nổi tiếng E.T.Bell đã từng gọi Fermat là "Hoàng tử của những người nghiệp dư". Bell cho rằng Fermat đã đạt được nhiều thành tựu toán học quan trọng hơn hầu hết các nhà toán học "chuyên nghiệp" cùng thời với ông.
Fermat rất say mê các công trình toán học của người Hy Lạp cổ đại, chính các công trình như Archimedes và Eudoxus đã gợi ý cho Fermat xây dựng khái niệm các phép toán giải tích.
Ông cố gắng tổng quát hóa các công trình toán học cổ điển và tìm ra nét mới trong kho tàng các phát minh đã bị chôn vùi từ rất lâu, như ông đã từng nói: "Tôi đã tìm được rất nhiều định lý đẹp vô cùng".
Mãi sau khi Fermat mất (12/1/1665), con trai ông mới in dần các công trình của cha kể từ năm 1670. Đến năm 1896, hầu hết các tác phẩm của Fermat được ấn hành thành 4 tập dày. Người ta đã vô cùng ngạc nhiên và khâm phục trước sự đóng góp lớn lao của ông.
Trong hình học, Fermat phát triển ra phương pháp tọa độ, lập phương trình đường thẳng và các đường cong bậc hai rồi chứng minh rằng các đường cong nọ chính là các thiết diện cônic. Trong toán giải tích, ông nêu các quy tắc lấy đạo hàm của hàm mũ với số mũ bất kỳ, tìm cực trị, tính tích phân những hàm mũ với số mũ phân số và số mũ âm.
Trong vật lý, chúng ta quá quen thuộc nguyên lý Fermat về truyền sáng, đó là một định luật quan trọng của quang học.
Nhưng đóng góp quan trọng nhất trong toán học của Fermat là lý thuyết số hiện đại, trong đó có 2 định lý nổi bật: định lý nhỏ Fermat và định lý lớn Fermat (định lý cuối cùng của Fermat).
Câu chuyện về định lý cuối cùng của Fermat là câu chuyện độc nhất vô nhị trong lịch sử toán học thế giới, khởi nguồn từ cổ đại với nhà toán học Pythagore.
Bài toán cuối cùng (sau này giới toán học gọi là Định lý cuối cùng của Fermat, hay Định lý lớn Fermat) có gốc từ định lý Pythagore: "Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông". Fermat thay đổi phương trình Pythagore và tạo ra một bài toán khó bất hủ.
Xét phương trình Pythagore: x2 + y2 = z2
Người ta có thể hỏi những nghiệm số nguyên của phương trình này là gì, và có thể thấy rằng: Có vô số nghiệm nguyên chẳng hạn (3,4,5) và (5,12,13).
Fermat khi đó xét dạng bậc ba của phương trình này: x3 + y3 = z3.
Đối với câu hỏi có thể tìm được nghiệm (nguyên) cho phương trình bậc ba này hay không? Fermat đã khẳng định là không. Thực ra, ông khẳng định điều đó cho họ phương trình tổng quát : xn + yn = zn với n là số nguyên lớn hơn 2. Đó là Định lý Fermat cuối cùng.
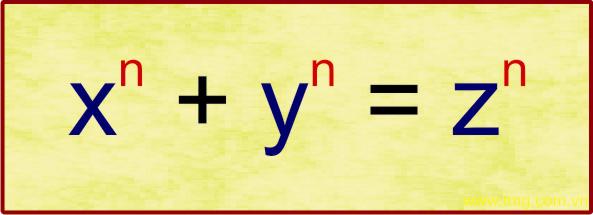
Gắn liền với định lý này là câu chuyện rất hay, đó là Fermat cho rằng không thể tìm được nghiệm (nguyên) cho phương trình bậc ba. Điều lý thú ở đây là phỏng đoán này được Fermat ghi bên lề một cuốn sách mà không chứng minh, nhưng có kèm theo dòng chữ: “Tôi có một phương pháp rất hay để chứng minh cho trường hợp tổng quát, nhưng không thể viết ra đây vì lề sách quá hẹp.”
Với những dòng viết tay đó, nhà toán học người Pháp Pierre de Fermat đã chính thức buông lời thách đố đối với thế hệ các nhà toán học sau ông. Nhiều nhà toán học đã dành cả cuộc đời để cố chứng minh định lý phát biểu nghe có vẻ hết sức đơn giản này.
Hành trình mấy trăm năm để giải lời thách đố, cùng với sự phức tạp của lời giải hàng trăm trang, từ bao thế hệ các nhà toán học đã làm người ta vừa nghi ngờ dòng ghi chú của Fermat, vừa tò mò, thán phục ông.
Trong lịch sử công cuộc tìm lời giải cho "Định lý cuối cùng của Fermat" có người phải tự tử và có những người tự lừa chính mình. Cuối cùng sau gần 4 thế kỷ, nhà toán học người Anh, Andrew Wiles cũng công bố lời giải độc nhất vô nhị vào mùa hè năm 1993 và bản chỉnh sửa cuối cùng vào năm 1995, với lời giải dài 200 trang.
Trung tâm Thông tin Tư liệu/TTXVN